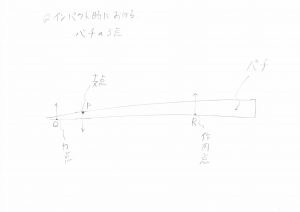
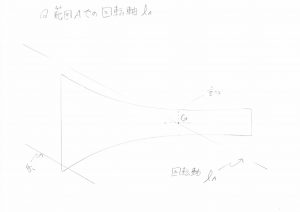
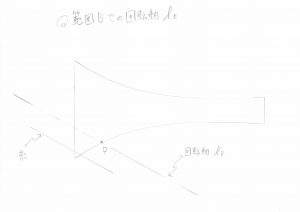
インパクトの瞬間に、バチはテコになっていると考えてみました。
バチにおける三点は、力点Q:糸からバチに加わる抗力の作用点 , 支点P:親指からバチに加える力の作用点 , 作用点R:指たちからバチに加える力の作用点。
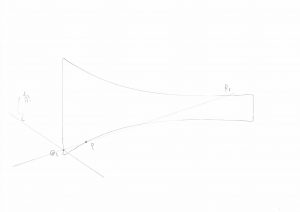
力点、作用点、としてますが、糸とバチ先は点でなく線で接しています。
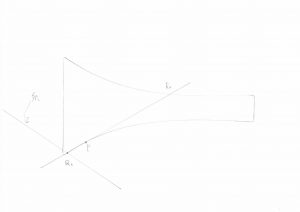
仮に力点がバチ先の端Q1に極端に寄っているとすると、
作用点はR1の位置になります。
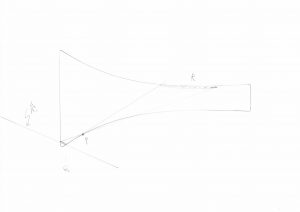
また、力点がバチ先の逆端Q2に極端に寄っているとすると、
作用点はR2の位置になります。
ですので、バチ先に接している糸に均一に力を加えたいなぁと思ったら、
ある程度の広さを持った範囲Rに、指たちからバチへ力を加えてやる必要があるかもしれません。
以上のことも、インパクトの瞬間のスナップのときに意識したほうがいいのかなぁ。
正直、スナップって何だろうと考えれば考えるほど袋小路に迷い込んでいる現状です。